STREDNÁ  PRIEMYSELNÁ  ŠKOLA  J.  MURGAŠA  BANSKÁ  BYSTRICA                          Elektrotechnické  laboratóriá

Odbor:

Dátum merania:

Trieda:

Dátum odovzdania:

Skupina:

Vyučujúci: doc.RNDr.Juraj Pančík, CSc.

Laboratórium:

Klasifikácia:

Známka:

Podpis:

Meno a priezvisko žiaka:

LABORATÓRNE  CVIČENIE  č. 33 Meranie sily so snímačom sily v mostíkovom zapojení (digitálna váha)

OBSAH:

1. Názov cvičenia a jednotlivých úloh.

2. Súpis prístrojov a pomôcok pri meraní.

3. Popis meracej metódy a schéma merania.

4. Tabuľky a grafy nameraných a vypočítaných hodnôt.

5. Vyhodnotenie merania.

1. NÁZOV CVIČENIA:

Meranie sily so snímačom sily v mostíkovom zapojení (digitálna váha)

Úlohy      a)

Oboznámte sa s hardvérovým a softvérovým riešenia meracieho prípravku

b)

Vykonajte merania hmotnosti pri rôznych hodnotách referenčných závaží pre mechaniku digitálnej váhy,  ktorá používa odporové snímače sily v mostíkovom zapojení. Použite referenčnú digitálnu váhu.

c)

Kalibračným stanovte počiatočný offset „Offset“ [ADU]  a prevodovú konštantu digitálnej váhy vyjadrenú v jednotkách [ADU/g]

d)

Vyjadrite linearitu modelu prevodovej charakteristiky digitálnej váhy (závislosť výstupnej veličiny signálu zo snímača sily [ADU]  na vstupnej veličine (hmotnosť, [g] ) )

e)

2.SÚPIS POUŽITÝCH PRÍSTROJOV

Prístroj – pomôcka

Typové označenie a rozsah

Výrobca

Inventárne číslo

1.

MP c.33 Merací prípravok pre meranie sily (digitálna váha)

2.

Kuchynská digitálna váha (max.5 kg, presnosť ±1g)

3.

Sada závaží z laboratória fyziky

Nedostatky pri hodnotení (zapíše vedúci merania  učiteľ):

3. Popis meracej metódy a schéma merania

Princíp merania sily. Ak sa pás vodivého kovu natiahne, stane sa tenším a dlhším, pričom obe zmeny vedú k zvýšeniu elektrického odporu od konca ku koncu. Naopak, ak sa pás vodivého kovu vystaví tlakovej sile (bez vybočenia), rozšíri sa a skráti. Ak sa tieto napätia udržiavajú v medziach pružnosti kovového pásika (aby sa pásik trvalo nedeformoval), pásik sa môže použiť ako merací prvok fyzikálnej sily, pričom veľkosť pôsobiacej sily sa odvodí z merania jeho odporu. Takéto zariadenie sa nazýva tenzometer. Tenzometre sa často používajú v strojárskom výskume a vývoji na meranie napätí, ktoré vznikajú v strojových zariadeniach. Jednou z oblastí použitia je testovanie komponentov lietadiel, kde sa na meranie napätia používajú malé tenzometrické pásy prilepené na konštrukčné prvky, spojovacie zariadenia a akékoľvek iné kritické komponenty draku lietadla. Väčšina tenzometrov je menšia ako poštová známka a vyzerá približne ako na obrázku Obrázok 1.

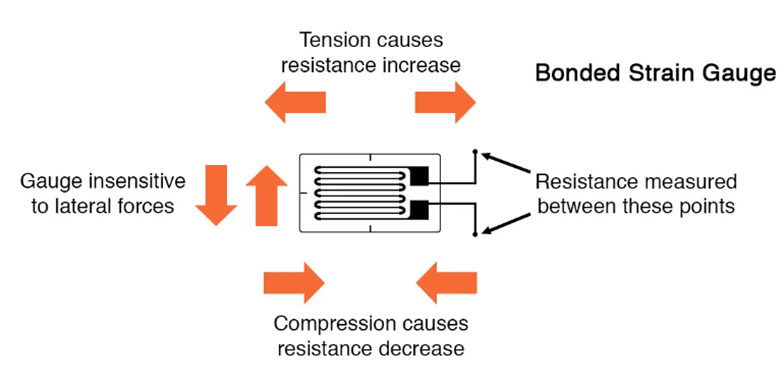
 Obrázok 1 Principiálna schéma snímača sily – tenzometra [1]

Odolnosť tenzometra. Typické odpory tenzometrov sa pohybujú od 30 Ω do 3 kΩ (bez napätia). Tento odpor sa môže zmeniť len o zlomok percenta pre celý rozsah sily meradla vzhľadom na obmedzenia vyplývajúce z elastických limitov materiálu meradla a skúšobnej vzorky. Sily dostatočne veľké na vyvolanie väčších zmien odporu by trvalo deformovali skúšobnú vzorku a/alebo samotné vodiče meradla, čím by sa meradlo ako meracie zariadenie zničilo. Preto, aby sme mohli tenzometer používať ako praktický prístroj, musíme merať veľmi malé zmeny odporu s vysokou presnosťou.

Mostíkový merací obvod

Takáto vysoká presnosť si vyžaduje mostíkový merací obvod. Na rozdiel od Wheatstonovho mostíka, ktorý využíva detektor nulovej rovnováhy a ľudskú obsluhu na udržiavanie rovnovážneho stavu, obvod tenzometrického mostíka indikuje meranú deformáciu stupňom nerovnováhy a na presné meranie tejto nerovnováhy využíva presný voltmeter v strede mostíka, viď.  Obrázok 2

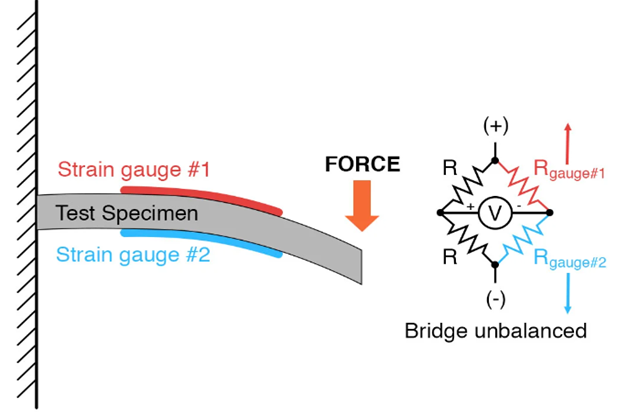
Obrázok 2 Rozváženie tzv. „half bridge“ tenzometra pod vplyvom záťaže (váženej hmotnosti v prípade digitálnych váh) [1]

Meracia metóda

Nami použitá meracia metóda vychádza z konštrukcie digitálnej váhy kde sa použil tzv „full bridge“ t.j. štvorica tenzometrov, viď. Obrázok 3.

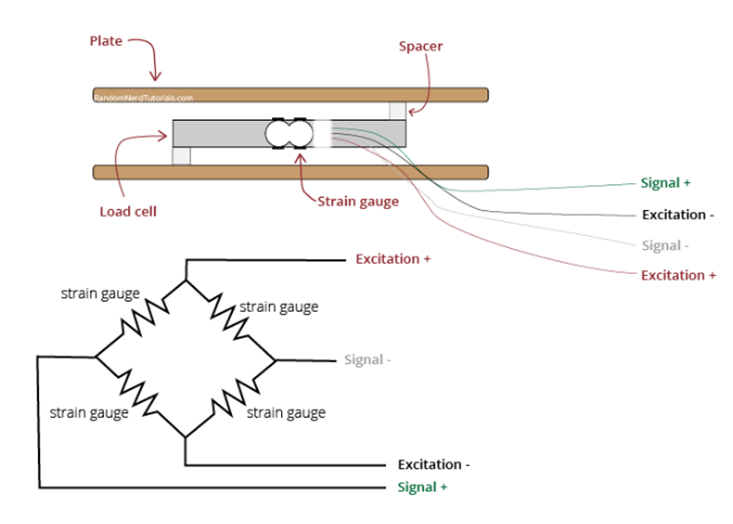
Obrázok 3 Mechanika digitálnej váhy a lokalizácia tenzometrov na hliníkovom nosníku s dvoma veľkými otvormi [2].

Merací systém

Merací systém pozostáva okrem spomínaných mechanických častí digitálnej váhy (hliníkový bloček s nalepenými tenzometrami v konfigurácii „full bridge“, polykarbonátové platne (horná a dolná)). Ďalším prvkom je zákaznícky obvod HX711 spoločnosti Avia [3], ktorý slúži ako „front end“ obvod, programovateľný zosilňovač, 24 bitový Sigma Delta ADC (analógovo digitálny prevodník) a komunikačno sériový interface (rozhranie) pre vyhodnocovací jednodoskový počítač typu ARDUINo UNO Rev.3, viď. Obrázok 4. Program v ARDUINO zabezpečil výpis získaných digitálnych údajov z HX711 tzv. 24 bit RAW dát (v jednotkách ADU) na sériovú linku čítanú terminálovým programom v počítači.  Program v ARDUINO dokázal vypočítať priemer z 10 hodnôt.     

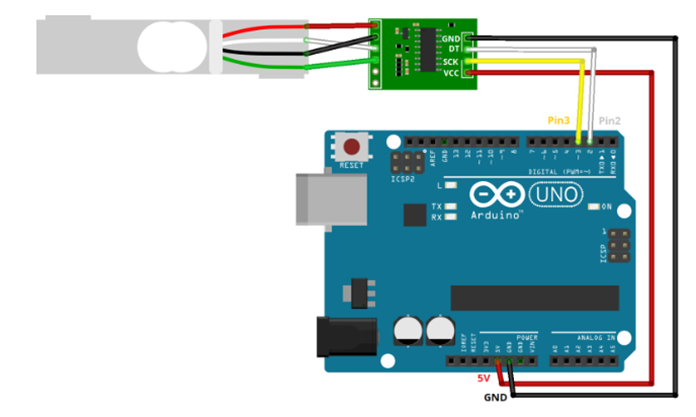
Obrázok 4 Bloková schéma meracieho systému na meranie sily v zostave digitálnej váhy [2]

4. Tabuľky a grafy nameraných a vypočítaných hodnôt.

Najprv sme vykonali  merania hmotnosti pri rôznych hodnotách referenčných závaží pre mechaniku digitálnej váhy,  ktorá používa odporové snímače sily v mostíkovom zapojení. Použili sme referenčnú kuchynskú digitálnu váhu a zistili sme maximálne 1g odchýlku od deklarovaných hmotností použitých závaží.   Vstupná tabuľka č.1 prezentuje výsledky váženia pre jednotlivé hmotnosti kalibračných závaží (viď. stĺpec „Hmotnosť kalibračných závaží [g]“ ). V stĺpci „Signál z ADC [ADU]“ sú zaznamenané údaje z 24 bit Sigma delta ADC. Následne po tomto meraní sme vykonali kalibráciu digitálnej váhy.  Kalibračným postupom sme stanovili  počiatočný offset „Offset“ [ADU]  (hodnota 153 647 ADU) a stanovili sme prevodovú konštantu digitálnej váhy (= 757 [ADU/g]) vyjadrenú v jednotkách [ADU/g] nasledovným výpočtom :

Kalibračný faktor [ADU/g] =

 (Signál z ADC [ADU] pre 100 g závažie – OFFSET [ADU]) / 100 g (referenčná záťaž)    (1)

 Tabuľka 1 Výsledky váženia pre jednotlivé hmotnosti kalibračných závaží

n	Hmotnosť kalibračných závaží [g]	Signál z ADC [ADU]	Kalibračný faktor [ADU/g]
1	0	153647
2	100	229330	757
3	200	304864	755
4	300	379454	746
5	400	454723	753
11	970	888471
12	1070	964282	758
13	1170	1039856	756
14	1270	1114524	747
15	1370	1189804	753

Grafom sme vyjadrili sme  linearitu modelu prevodovej charakteristiky digitálnej váhy (závislosť výstupnej veličiny signálu zo snímača sily [ADU]  na vstupnej veličine (hmotnosť, [g] ) ) – rovnica lineárnej závislosti (y = 756,83x + 153647) bola vypočítaná EXCELOM vrátane linearizačného koeficientu R² = 1. Táto hodnota koeficientu hovorí o vysokom stupni lineárnej odozvy snímačov sily  v našej mechanickej zostave digitálnej váhy.

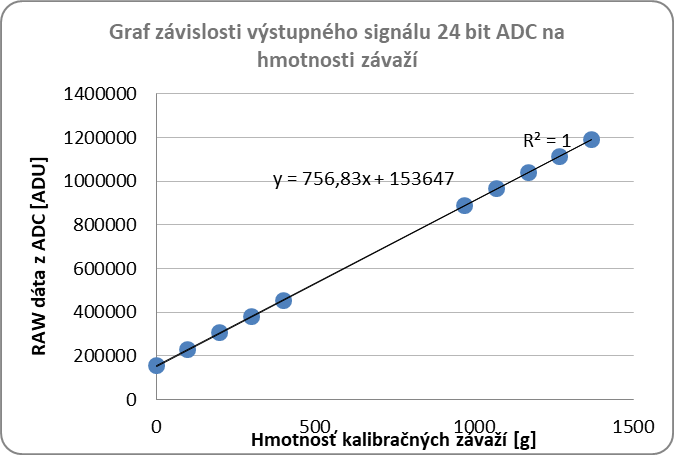
Obrazok 5 Linearitu modelu prevodovej charakteristiky digitálnej váhy

5. Vyhodnotenie merania.

Oboznámili sa s hardvérovým a softvérovým riešením  meracieho prípravku – zaregistrovali sme veľký počet digitalizačných úrovní N použitého ADC (N=24) čo zrejme súvisí s potrebou získania vysokého odstupu signál šum v systémovom riešení spracovania signálu z tenzometrov. Vykonali sme  merania hmotnosti pri rôznych hodnotách referenčných závaží pre mechaniku digitálnej váhy a pri tomto sme použite referenčnú digitálnu váhu s presnosťou ±1g. Samotné nami použité závažia vykazovali taktiež tento rozptyl hodnôt hmotností ±1g. Kalibračným postupom s hmotnosťou kalibračného závažia  100 g sme stanovili počiatočný offset „Offset“ [ADU]  a prevodovú konštantu digitálnej váhy 757  vyjadrenú v jednotkách [ADU/g]. Kalibračné závažie by malo byť na hodnote 80% maximálnej povolenej záťaže hliníkového nosníka (v našom prípade 3kg) t.j. 2,4kg  – my sme použili nám dostupné 100g závažie.  Pomocou grafu na Obrazok 5 sme vyjadrili linearitu modelu prevodovej charakteristiky digitálnej váhy (závislosť výstupnej veličiny signálu zo snímača sily [ADU]  na vstupnej veličine (hmotnosť, [g])) pomocou rovnica lineárnej závislosti (y = 756,83x + 153647) bola vypočítaná EXCELOM vrátane linearizačného koeficientu R² = 1. Táto hodnota koeficientu hovorí o vysokom stupni lineárnej odozvy snímačov sily  v našej mechanickej zostave digitálnej váhy.

6. Informačné zdroje

[1]   https://www.allaboutcircuits.com/textbook/direct-current/chpt-9/strain-gauges/

[2]   https://randomnerdtutorials.com/arduino-load-cell-hx711/#more-110379

[3]   https://community.infineon.com/gfawx74859/attachments/gfawx74859/CodeExamples/546/7/HX711_v0_0_B.pdf